The term ‘self-organizing map’ might conjure up a militaristic image of data points marching towards their contingents on a map, which is a rather apt analogy of how the algorithm actually works.
A self-organizing map (SOM) is a clustering technique that helps you uncover categories in large datasets, such as to find customer profiles based on a list of past purchases. It is a special breed of unsupervised neural networks, where neurons (also called nodes or reference vectors

Figure 1. SOM grids can either be rectangular or hexagonal. Each square or hexagon is a neuron.
Let’s see a visual example of how SOM works. The accompanying SOM code in R is on our GitHub page.
A Visual Walkthrough
One example of a data type with more than two dimensions is color. Colors have three dimensions, typically represented by RGB (red, green, blue) values. In this example, we will see how SOM can distinguish two color clusters.
Data Generation
We picked two colors—yellow and green—around which to generate random samples to form two clusters. We can visualize our color clusters using blue and green values, which are the dimensions along which the clusters are most differentiated.
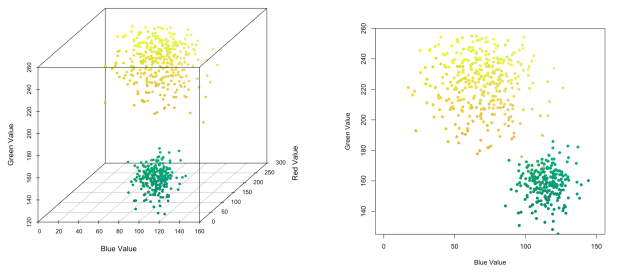
Figure 2. Two color clusters of yellow and green, in 3D and 2D spaces.
Data Analysis
It’s time to build our SOM. We used an 8 x 8 rectangular grid, so there were 64 neurons in total. Initially, neurons in the SOM grid start out in random positions, but they are gradually massaged into a mould outlining the shape of our data. This is an iterative process, which we can watch from the animated GIF below:

Figure 3. Animated GIF showing how an SOM grid evolves to take the shape of our data. Note that the visualization is a top-down view of the data, and the neurons are actually moving in three dimensions
We can see that the grid’s shape stabilizes after a couple of hundred iterations. To check that the algorithm has converged, we can plot the evolution of the SOM’s energy—initially, the SOM evolves rapidly, but as it reaches the approximate shape of the data, the rate of change slows down.

Figure 4. Evolution of the SOM’s energy. It took about 150 iterations for neurons in the SOM grid to stabilize.
To get an overview of how many data points each neuron corresponded to, we can plot a frequency map of the grid, shown below. Each neuron is represented by a square, and the pink region within the square represents the relative number of data points that neuron is positioned closest to—the larger the pink area, the more data points represented by that neuron.

Figure 5. Frequency map of neurons in an 8 x 8 SOM grid.
From the frequency map, we can see a clear divide separating a top left neuron cluster from a smaller bottom right cluster. This divide is represented by the neurons in-between with small or no pink squares.
U-matrix, which visualizes how much neurons differ from each other in 2-dimensional space. When two neurons correspond to vastly different sets of data points, they would be separated by a larger distance, denoted by a pink color. On the other hand, neurons representing similar data points are separated by shorter distances, denoted by a blue color.

Figure 6. U-matrix showing similarity and dissimilarity between neurons. Useful for identifying clusters.
Comparing the sizes of neuron clusters, we can infer that the bigger cluster in the top left probably corresponds to the larger group of yellow data points, leaving the smaller bottom right cluster to correspond to green data points.

Figure 7. Radar plots showing the aggregated profile of each neuron, as determined by their constituent data points.
t-SNE). While the 2-dimesional space is popular due to its use for visualization, the SOM is a general dimension reduction technique that can simplify a dataset to any number of variables, and is closely related to what we learned previously on principal components analysis.
Now that you’ve seen how SOM effectively identifies clusters, we will explain how it works under the hood.
How does SOM Work?
So how does the SOM grid learn the shape of our data? Well, this is done in an iterative process, which is summarized in the following steps, and visualized in the animated GIF below:
Step 0: Randomly position the grid’s neurons in the data space.
Step 1: Select one data point, either randomly or systematically cycling through the dataset in order
Step 2: Find the neuron that is closest to the chosen data point. This neuron is called the Best Matching Unit (BMU).
Step 3: Move the BMU closer to that data point. The distance moved by the BMU is determined by a learning rate, which decreases after each iteration.
Step 4: Move the BMU’s neighbors closer to that data point as well, with farther away neighbors moving less. Neighbors are identified using a radius around the BMU, and the value for this radius decreases after each iteration.
Step 5: Update the learning rate and BMU radius, before repeating Steps 1 to 4. Iterate these steps until positions of neurons have been stabilized.

Figure 8. Iterative process of an SOM.
Another feature that we need to validate is the optimal number of neurons in the grid. Recall that because each neuron has multiple data points associated with it, it can be treated as a mini-cluster. We can thus validate each neuron to see if its associated data points correspond to known sub-clusters of, say, consumer profiles. In order for such clusters to be distilled however, there should be fewer neurons than data points, so that similar data points can be mapped to each neuron.
One thing to note before we apply SOM: Variables measured in different units could interfere with the speed and accuracy of our analysis. For example, a variable measured in centimeters would have a value 100 times larger than the same one measured in meters. To prevent any variable from overpowering the others, we need to standardize
Limitations of SOM
Does not handle categorical variables well. To obtain a scatterplot with good data spread to identify clusters, SOM will have to assume that all variables in the dataset are continuous. Plotting categorical values will result in data points lining up at discrete values instead of spreading across the plot.
. A dataset with more variables would require longer times to calculate distances and identify BMUs. To expedite computations, we could improve our initial positions of neurons from a random state to a more informed approximation with the help of a simpler dimension reduction technique, such as principal components analysis. By starting the neurons off closer to the data points, less time would be needed to move them to their optimal locations.
Potentially inconsistent solutions. As initial positions of neurons differ each time the SOM analysis is run, the eventual SOM map generated will also differ. Sometimes, overly large clusters may be split up and represented by two separate clusters of neurons. Therefore, before concluding on the number of clusters, the SOM analysis can be repeated to check for consistency, and resulting clusters should be validated against actual cases.
Summary
- SOMs are best for datasets with continuous variables, and it should be repeated to check for consistency. Resulting clusters should also be validated.
Did you learn something useful today? We would be glad to inform you when we have new tutorials, so that your learning continues!
Sign up below to get bite-sized tutorials delivered to your inbox:
Copyright © 2015-Present Algobeans.com. All rights reserved. Be a cool bean.


great post
LikeLike
Hi, great post! Can I ask for an explanation on the R code where you remove the crisscross pts? How do we know that these points will crisscross? The logic written makes it so that for every pt %% 8 == 0 or 1 a value +/- 1 from the pt will be removed from the pt_neighbor variable.
LikeLike
that is awesome!
LikeLike
Great tutorial. How do you define the energy for the SOM?
LikeLike